坐标系,高斯模式的坐标系为:以排放点(无界点源或地面源)或高架源排放点在地面的投影点为原点,平均风向为
x轴,y 轴在水平面内垂直于x 轴,y
轴的正向在 x 轴的左侧,z
轴垂直于水平面,向上为正方向。即为右手坐标系。在这种坐标系中,烟流中心或与
x 轴重合(无界点源),或在 xoy,面的投影为 x 轴
(高架点源)。
高斯模式的四点假设,高斯模式的四点假设为:(1)污染物在空间
yoz 平面中按高斯分布(正态分布),在 x方向只考虑迁移,不考虑扩散;(2)在整个空间中风速是均匀、稳定的,风速大于lm/s;(3)源强是连续均匀的;(4)在扩散过程中污染物质量是守衡的。对后述的模式只要没有特殊指明,以上四点假设条件都是遵守的。图5-5
示高斯模式的坐标系和基本假设。
(1)无限空间连续点源的高斯模式为:
由正态分布的假设,写出下风向任意点(x、y、z)污染物平均浓度分布的函数为:
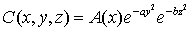
由概率统计理论可以写出方差的表达式:
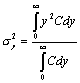 ;
;
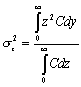
由假设(4)可写出:

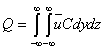
上述四个方程,组成一个方程组,源强Q、平均风速u、标准差σy、σz为已知量,浓度C、待定函数A(x)、待定系数a
和 b为未知量。因此,方程组可求解。
将式(5—19)依次代入式(5—20)的两式中,积分后得到:
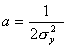 ;
;
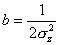
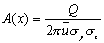
上式合并,得无界空间连续点源高斯模式:
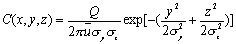
图5-6
高架连续点源高斯模式的推导
(2)架连续点源的高斯模式
高架连续点源的扩散问题,必须考虑到地面对扩散的影响。根据前述假设(4),可以认为地面象镜面那样,对污染物起着全反射的作用。按照全反射原理,可以用像源法来处理这类问题。
如图5-6所示,我们可以把
P
点的污染物浓度看成是两部分之和。一部分是不存在地面影响情况下,
P
点所具有的污染物浓度;另一部分是由于地面反射作用所增加的污染物浓度。这相当于实源在地面下的
-H 位置处的像源,按照无限空间连续点源模式,在P点所造成的污染物浓度。
首先看实源的作用:P
点在以实源排放点(有效源高处)为原点的坐标系(无限空间)中的铅直坐标(距烟流中心线的铅直距离)为(z-H)。当不考虑地面影响时,浓度按式
(5-24)计算,它在
P 点所造成的污染物为:
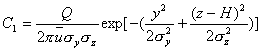
像源的作用:P
点在以像源排放点(负的有效源高处)为原点的坐标系(无限空间)中的铅直坐标(距像源产生的烟流中心线的铅直距离)为(z+H)。它在
P 点产生的污染物浓度也按式(5-24)计算,它在 P
点所造成的污染物为:
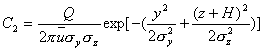
P
点的实际污染物浓度应为实源和像源作用之和,即
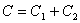
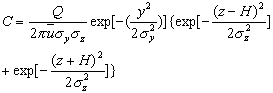
上式即为高架连续点源正态分布假设下的扩散模式,由这一模式可求出下风向任一点的污染物浓度。按照这一普适公式,如果 H
=0,则对应于地面源的情况;如果z=0,则对应于连续点源作用下,地面处的污染物浓度情况;如果 z=0且 y=0,则对应于点源作用下,正风向轴线上,地面处的污染物浓度情况;在实施环境评价时,应特别关注这样一些特殊情况。